ポーカーの役の確率

全ての役が「確率通りの強さ設定」
になっているのだろうか？

ポーカーをしたことがある方は、
こんなことを思ったことはありませんか？

今回はそんな疑問を数学的に解説していきましょう。

ポーカーの役と確率

では、それぞれの役が成立する確率を、
役の強さが強い順に求めてみましょう。

トランプはジョーカーを除く52枚だけ。
求める確率は「最初に配られた5枚で役が揃う確率」とします。

はじめに、52枚の中から5枚配られる組み合わせ総数は、

$$ {}_{52} C_5 =2598960 $$

2598960通りとなります。

ロイヤルストレートフラッシュ

ロイヤルストレートフラッシュは、
同じマークで、かつ「10, J, Q, K, A」からなる役です。

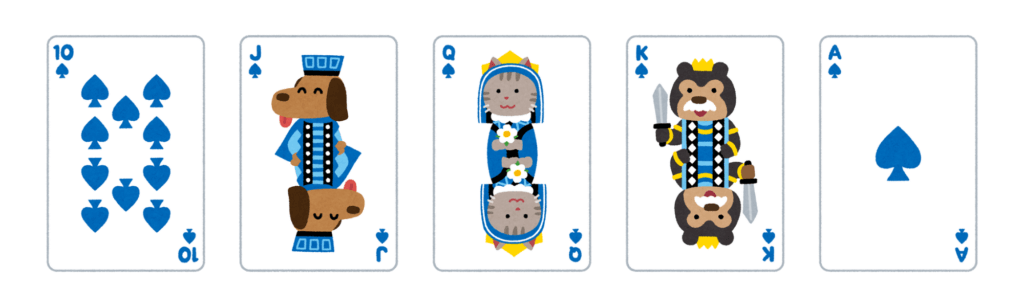
これは、1つのマークにつき1組しかありえないので、
ロイヤルストレートフラッシュの出現確率は、

$$ \frac{4}{2598960} = \frac{1}{649740} $$

つまり、約0.00015%となります。

ストレートフラッシュ

ストレートフラッシュは、
同じマークで、かつ連続した数字5枚からなる役です。

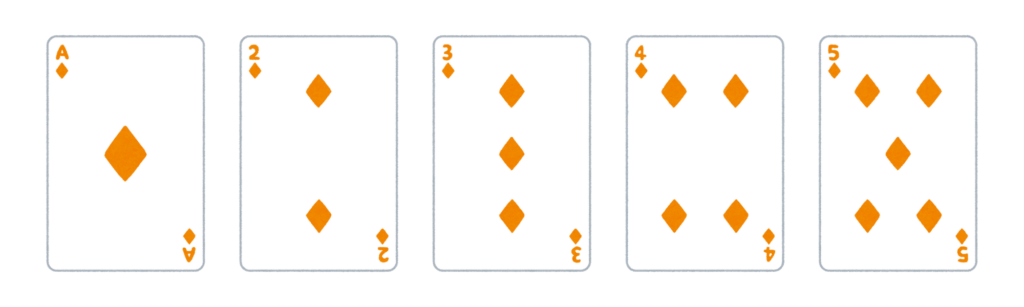
連続した数字はロイヤルストレートフラッシュを除き、
「A, 2, 3, 4, 5」から「9, 10, J, Q, K」まで9通り。

これが4つのマークであるので、ストレートフラッシュの出現確率は、

$$ \frac{36}{2598960} = \frac{3}{216580} $$

つまり、約0.0014%となります。

フォーカード

フォーカードは、同じ数字が4枚と、その他1枚からなる役です。

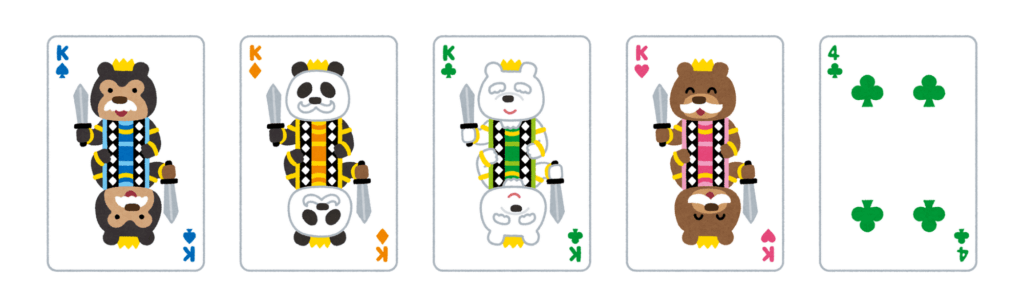
同じ4枚の組み合わせは、A～Kまでの13通りがあり、
その他1枚はそれ以外の48枚から選ばれるので、

$$ 13×48＝624 $$

624通りあります。

よって、フォーカードの出現確率は、

$$ \frac{624}{2598960} = \frac{1}{4165} $$

つまり、約0.024%となります。

フルハウス

フルハウスは、同じ数字3枚と、同じ数字2枚からなる役です。

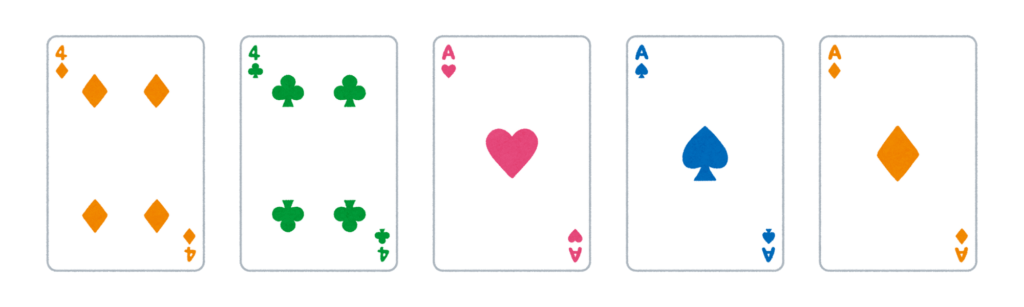
上の例で考えると、
4枚のKから3枚と、4枚のQから2枚選ぶ場合の数は、

$$ {}_{4} C_3 × {}_{4} C_2=24 $$

24通りになります。

KとQを使って、逆にQが3枚と、Kが2枚の組み合わせもあるので、
同じ数字を使った組み合わせは48通りになります。

最後に13枚の中から2種類の数字を選ぶ組み合わせは、

$$ {}_{13} C_2=78 $$

78通りなので、フルハウスの出現確率は、

$$ \frac{48×78}{2598960} = \frac{6}{4165} $$

つまり、約0.14%となります。

フラッシュ

フラッシュは、同じマーク5枚からなる役です。

1つのマークが13枚あるので、その中から5枚選ぶ組み合わせは、

$$ {}_{13} C_5=1287 $$

1287通り。

これが4つのマークでありえるので、
4倍して全部で5148通りとなります。

ただし、この中には
「ロイヤルストレートフラッシュ」
「ストレートフラッシュ」
も含まれているので、これを除くと、

$$ 5148-4-36=5108 $$

5108通りなので、フラッシュの出現確率は、

$$ \frac{5108}{2598960} = \frac{1277}{649740} $$

つまり、約0.2%となります。

ストレート

ストレートは、連続した数字5枚からなる役です。

上の例で考えると、
4つのマークのA、2、3、4、5からそれぞれ1枚選ぶ組み合わせは、

$$ 4^5=1024 $$

1024通り。

これをAから始まるものから10から始まるものまでを考えるので、

$$ 1024×10=10240 $$

10240通り。

ただし、この中には
「ロイヤルストレートフラッシュ」
「ストレートフラッシュ」
も含まれているので、これを除くと、

$$ 10240-4-36=10200 $$

10200通りなので、フラッシュの出現確率は、

$$ \frac{10200}{2598960} = \frac{5}{1274} $$

つまり、約0.39%となります。

スリーカード

スリーカードは、同じ数字3枚と、他の数字2枚からなる役です。

同じ数字の4枚の中から3枚選び、
それ以外の48枚から2枚を選ぶ組み合わせは、

$$ {}_{4} C_3 × {}_{48} C_2=4512 $$

4512通り。

これが13枚の数字であり得るので、

$$ 4512×13＝58656 $$

ただし、この中には
「フルハウス」も含まれているので、これを除くと、

$$ 58656-3744=54912 $$

54912通りなので、スリーカードの出現確率は、

$$ \frac{54912}{2598960} = \frac{88}{4165} $$

つまり、約2.11%となります。

ツーペア

ツーペアは、同じ数字2枚のペアが2セットと、他の数字1枚からなる役です。

4枚ある数字の中から2枚選ぶのを2回、
その数字以外の44枚から1枚選ぶ組み合わせは、

$$ {}_{4} C_2 × {}_{4} C_2 × 44=1584 $$

1584通り。

2つのペアは、13枚ある数字の中から2種類を選ぶので、
ツーペアの組み合わせの数は、

$$ {}_{13} C_2 × 1584=123552 $$

123552通りなので、ツーペアの出現確率は、

$$ \frac{123552}{2598960} = \frac{198}{4165} $$

つまり、約4.75％となります。

ワンペア

ワンペアは、同じ数字2枚のペアが1セットと、他の数字3枚からなる役です。

4枚ある数字の中から2枚選び、
その数字以外の48枚から1枚選び、
さらにその数字以外の44枚から1枚選び、
さらにその数字以外の40枚から1枚選ぶ組み合わせは、

$$ {}_{4} C_2 × 48 × 44 × 40=506880 $$

506880通り。

ただし、ペアになる数字は13枚あり、
ペアでないカードの順序は無視してよいので、
※（2, 3, 4）（2, 4, 3）（3, 2, 4）（3, 4, 2）（4, 2, 3）（4, 3, 2）は同じ。

ワンペアの組み合わせの数は、

$$ 506880 × 13 ÷ 3! = 1098240 $$

1098240通りなので、ワンペアの出現確率は、

$$ \frac{1098240}{2598960} = \frac{352}{833} $$

つまり、約42.3％となります。

ノーペア

ノーペアは、上記のどの役も揃っていない状態です。

つまり、ノーペアの組み合わせ数は、
組み合わせ総数から全役の組み合わせ数を引いて、1302540通り。

よって、ノーペアの出現確率は、

$$ \frac{1302540}{2598960} = \frac{1277}{2548} $$

つまり、約50.1％となります。

まとめ

結果はこの通り。

・ロイヤルストレートフラッシュ
　　　　　　　：約0.00015%
・ストレートフラッシュ
　　　　　　　：約0.0014%
・フォーカード：約0.024%
・フルハウス　：約0.14%
・フラッシュ　：約0.2%
・ストレート　：約0.39%
・スリーカード：約2.11%
・ツーペア　　：約4.75%
・ワンペア　　：約42.3%
・ノーペア　　：約50.1%

配られた時点での組み合わせに関しては、
全ての役が出現確率順に並んでいることが分かりました。

ただし、実際は数ターンのカード交換があるため、
「フルハウス」はペアをキープした状態で狙えるのに対して、
「ストレート」はペアを解消する必要があったりと、
手持ちの数やマークによって戦術は大きく変わってきます。